Given:
The composite figure consists of a rectangle and a hemisphere.
The length of the rectangle is 11 mm.
The width of the rectangle is 9 mm.
The height of the rectangle is 6 mm.
We need to determine the volume of the composite figure.
Volume of the rectangle:
The volume of the rectangle can be determined using the formula,
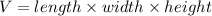
Substituting the values, we get;
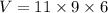
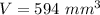
Thus, the volume of the rectangle is 594 mm³
Volume of the half of the cylinder:
The volume of the half of the cylinder is given by the formula,
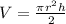
Radius of the cylinder =
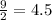
Height of the cylinder = 11 mm
Substituting the values, we get;
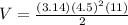
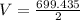
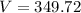
Thus,the volume of the half of the cylinder is 349.72 mm³
Volume of the composite figure:
The volume of the composite figure can be determined by adding the volume of the rectangle and the volume of the half of the cylinder.
Thus, we have;
Volume = Volume of rectangle + Volume of half of the cylinder
Substituting the values, we get;
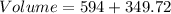

Rounding off to the nearest whole number, we get;
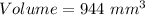
Thus, the volume of the composite figure is 944 mm³
Hence, Option d is the correct answer.