Question

Which of the following is equivalent to the polynomial given below?

x^2+6x+20

PLEASE HURRY!!

Answer 1

Given:

Polynomial
`x^2+6x+20`

To find:

The equivalent polynomial.

Solution:

`x^2+6x+20=0`

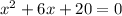
a = 1, b = 6, c = 20

Using quadratic formula:

`$x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

`$x=\frac{-6 \pm \sqrt{6^(2)-4 \cdot 1 \cdot 20}}{2 \cdot 1}`

`$x=\frac {-6 \pm √(-44)}{2}`

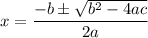
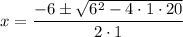
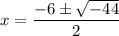
44 can be written as 11 × 4 = 11 × 2²

`$x= \frac {-6 \pm √(-11 * 2^2)}{2}`

`$x= \frac {-6 \pm2 √(-11 )}{2}`

`$x =(2(-3 \pm i √(11)))/(2)`

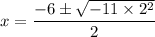
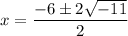
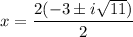
Cancel the common factor 2.

`$x =-3 \pm i √(11)`

`$x =-3 + i √(11)`,
`$x =-3 - i √(11)`

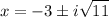
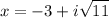Convert into factors.

`$x -(-3 + i √(11))=0`,
`$x -(-3 - i √(11))=0`

`$x + (3 - i √(11))=0`,
`$x + (3 + i √(11))=0`

`$(x + (3 - i √(11)))(x + (3 + i √(11)))`

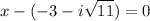
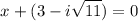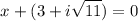
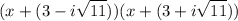
Interchange their positions.

`$(x + (3 + i √(11)))(x + (3 - i √(11)))`

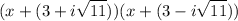
Therefore option B is the correct answer.

The equivalent polynomial is
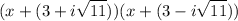`$(x + (3 + i √(11)))(x + (3 - i √(11)))`.