Answer:
Here's what I get
Explanation:
a) x² = x - b
I plotted the graphs of y = x² - x + b with different values of b and found:
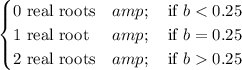
You can see three specific cases in Fig.1.
b) x² = bx - 1
I plotted the graphs of y = x² - bx + 1 with different values of b and found:

You can see five specific cases in Fig. 2.