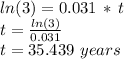Question

If $48,000 is invested in an account earning 3.1% interest compounded continuously, determine how long it will

take the money to triple. Round to the nearest year. Use the model A = Pert where A represents the future value
of P dollars invested at an interest rate r compounded continuously for t years.

Answer 1

It will take about 35.439 years to triple.

Explanation:

Recall the formula for continuously compounded interest:

`A=P\,e^(r*t)`

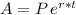
where "A" is the total (accrued or future) accumulated value, "r" is the rate (in our case 0.031 which is the decimal form of 3.1%), "P" is the principal, and "t" is the time in years (our unknown).

Notice also that even that the final amount we want to get is three times $48,000. So our formula becomes:

`3\,*\,48,000=\,48,000\,\,e^(0.031\,*t)\\(3\,*\,48,000)/(48,000) =e^(0.031*t)\\3=e^(0.031*t)`

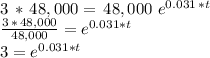
Now,in order to solve for "t" (which is in the exponent, we use logarithms:

`ln(3)=0.031\,*\,t\\t=(ln(3))/(0.031) \\t=35.439 \,\,years`