Given:
Given that AB is a tangent to circle C.
The length of AB is (2r -1)
The length of AC is (r + 1) + r
The length of BC is r.
We need to determine the circumference of the circle C.
Value of r:
The value of r can be determined using the Pythagorean theorem.
Thus, we have;
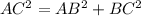
Substituting the values, we have;
![[(r+1)+r]^2=(2r-1)^2+r^2](https://img.qammunity.org/2021/formulas/mathematics/high-school/p85f7ndp7ib3ukc2ju43213iauttcl930z.png)
Simplifying, we have;

Expanding the terms, we get;
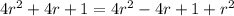
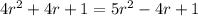
Simplifying the values, we have;
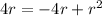
Adding both sides of the equation by 4r, we get;
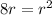
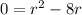
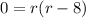
Thus,
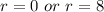
Since, the radius of the circle cannot be 0.
Hence, the radius of the circle is 8.
Circumference of the circle:
The circumference of the circle can be determined using the formula,
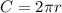
Substituting r = 8, we get;
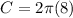
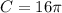
Thus, the circumference of the circle is 16π
Hence, Option A is the correct answer.