Question

Find the polar equation of the conic with the focus at the pole, directrix x = -5, and eccentricity 2.

Answer 1

B

Explanation:

Answer 2

Given:

Directrix x = -5 and eccentricity = 2

To find:

The polar equation of the conic.

Solution:

Eccentricity = 2 > 0

Therefore the conic must be a hyperbola.

Directrix is vertical (at x = -5) and the vertical directrix is located to the left of the pole.

So that the equation is of the form:

`$r=(e p)/(1-e \cos \theta)`

Since the eccentricity of this hyperbola is 1

The distance between the pole and directrix is

p = |-5|= 5

Substitute these in the above equation.

`$r=((2)(5))/(1-2 \cos \theta)`

`$r=(10)/(1-2 \cos \theta)`

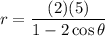
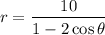
The polar equation of the conic is
`r=(10)/(1-2 \cos \theta)` hyperbola.