Question

Can you find GHJ AND GIJ FOR ME PLEASE

Answer 1

Given:

Circle with center O.

To find:

The measurement of the angle GHJ.

Solution:

The arc measure of full circle is 360°.

m(ar GJ) + m(ar JI) + m(ar IH) + m(ar HG) = 360°

m(ar GJ) + 115° + 31° + 68° = 360°

m(ar GJ) + 214° = 360°

Subtract 214° from both sides.

m(ar GJ) + 214° - 214°= 360° - 214°

m(ar GJ) = 146°

The measure of inscribed angle is half the intercepted arcs.

`$\Rightarrow m\angle GHJ = (1)/(2) m(ar \ GJ)`

`$\Rightarrow m\angle GHJ = (1)/(2) (146^\circ)`

`$\Rightarrow m\angle GHJ =73^\circ`

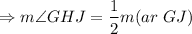
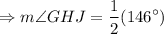
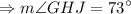
The measure of angle GHJ is 73°.