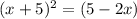Answer:
Raising both sides to the second power will eliminate only one rational exponent
Explanation:
we have
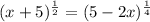
If raising both sides to the 2nd power
![[(x+5)^{(1)/(2)}]^2=[(5-2x)^{(1)/(4)}]^2](https://img.qammunity.org/2021/formulas/mathematics/high-school/xw8yrporvmalrtz5kc2h3cqu057i1degt3.png)
Remember the property of exponents
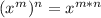
![x^{(m)/(n)}=\sqrt[n]{x^m}](https://img.qammunity.org/2021/formulas/mathematics/high-school/37ewcx8gwtesn9n1qkefzw4u7660b8ubkj.png)
so
Multiply the exponents
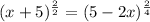
Simplify
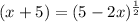
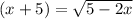
therefore
Raising both sides to the second power will eliminate only one rational exponent
To eliminate both rational exponents, both sides must be raised to the fourth power
so
![[(x+5)^{(1)/(2)}]^4=[(5-2x)^{(1)/(4)}]^4](https://img.qammunity.org/2021/formulas/mathematics/high-school/e2tz5pa8qvcdcwflyzzyl0qjhjnn5cuns6.png)

simplify