Question

Each student was asked to record and report the amount of money they spent on text books in a semester. The sample of 130 students resulted in the average of $422 and a standard deviation of $57. Find a 99% confidence interval for the mean amount of money spent by collage students on textbooks

Answer 1

Answer: (409.36, 434.64)

Explanation:

When population standard deviation is unknown and sample is not so large , then the formula to find the confidence interval for population mean is given by :-

`\overline{x}\pm t^*(s)/(√(n))`

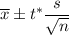
, where
`\overline{x}`= sample mean , n = sample size , s= sample population standard deviation, t*= two tailed critical value.

As , per given ,
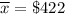`\overline{x}=\$422`, s=$57, n=130

For 99% confidence ,
`\alpha=0.01`

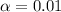
By t-distribution table , t-value for
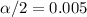`\alpha/2=0.005` (two tailed) and df =129 [∵df=n-1] would be

t*=2.6145

Now , the 99% confidence interval for the mean amount of money spent by collage students on textbooks will be :

`422\pm (2.6145)(57)/(√(139))`

`422\pm (2.6145)(4.834677)`

`422\pm 12.640263`

`(422- 12.640263,\ 422+12.640263)\\\\=(409.359737,\ 434.640263)\approx(409.36,\ 434.64)`

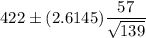
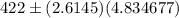
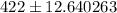
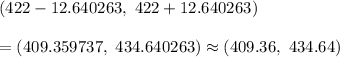
Hence, a 99% confidence interval for the mean amount of money spent by collage students on textbooks will be (409.36, 434.64).