Question

A rectangular prism with a volume of 333 cubic units is filled with cubes with side lengths of \dfrac14 4 1 ​ start fraction, 1, divided by, 4, end fraction unit. How many \dfrac14 4 1 ​ start fraction, 1, divided by, 4, end fraction unit cubes does it take to fill the prism?

Answer 1

192 cubes

Explanation:

Answer 2

192 unit cubes.

Explanation:

Let n represent number of cubes with each side 1/4 unit.

We have been given that a rectangular prism with a volume of 3 cubic units is filled with cubes with side lengths of 1/4 unit. We are asked to find the number of cubes that will fill that prism.

First of all, we will find volume of each cube.

`\text{Volume of cube}=\text{Side length}^3`

`\text{Volume of cube}=((1)/(4)\text{ unit})^3`

`\text{Volume of cube}=(1^3)/(4^3)\text{ unit}^3`

`\text{Volume of cube}=(1)/(64)\text{ unit}^3`

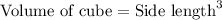
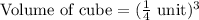
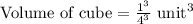
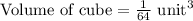
The volume of rectangular prism will be equal to volume of n cubes.

`\text{Volume of n cubes}=\text{Volume of rectangular prism}`

`n* (1)/(64)\text{ Unit}^3=3\text{ Unit}^3`

`n* (1)/(64)=3`

`n* (1)/(64)* 64=3* 64`

`n=192`

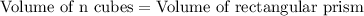
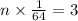
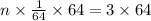
Therefore, it will take 192 unit cubes to fill the prism.