Question

Please Help! Thanks!

Triangle S R Q is shown. Angle S R Q is a right angle. An altitude is drawn from point R to point T on side S Q to form a right angle. The length of S T is 9, the length of T Q is 16, and the length of R Q is x.
What is the value of x?

12 units
15 units
20 units
24 units

Answer 1

20 units

Explanation:

Triangles SRQ and RTQ are similar figures

x/(9+16) = 16/x

x² = 16×25

x = 4×5

x = 20

Answer 2

C, 20 units

Explanation:

We see that both angles QRS and QTR are 90 degrees. In addition, angles SQR and RQT are equivalent (because they're both angle Q).

By AA Similarity, we know that triangle QTR is similar to triangle QRS.

With this similarity in mind, we can look at the ratios of corresponding lengths to set up a proportion. QR from triangle QTR is the hypotenuse, and it corresponds to hypotenuse QS from triangle QRS. So, we can write the ratio x/(9 + 16) = x/25.

Now, we see that long leg QT of triangle QTR corresponds to long leg QR of triangle QRS. So, another ratio we can write is: 16/x.

Finally, we set these two ratios equal to each other:

`(x)/(25) =(16)/(x)`

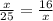
Cross-multiplying, we get:
`x^(2) =16*25=400`.

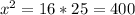Thus, x =
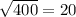`√(400) =20`. The answer is C, 20 units.

Hope this helps!