Answer:
DC = 39
Explanation:
From inspection of the diagram:
- EA is tangent to both circles
- DE is the radius of circle D
- CA is the radius of circle C
The tangent of a circle is always perpendicular to the radius, therefore:
DE ⊥ EA and CA ⊥ EA
As ∠DEB and ∠BAC are both 90°, then DE is parallel to CA.
Therefore, ∠DBE and ∠ABC are vertically opposite angles, and are therefore equal.
As triangles ΔBED and ΔBAC have two pairs of corresponding congruent angles, the triangles are similar.
Therefore:
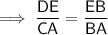
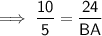

Using Pythagoras' Theorem for ΔBED to find DB:
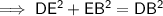
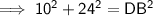
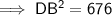
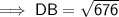
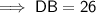
Using Pythagoras' Theorem for ΔBAC to find BC:

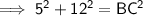
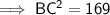
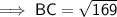

Therefore, the distance between the center of the circles DC is:
