Question

Jack lives east of NJH and finn lives west of NJH. Jack leaves right after school and rides his bike home at an average speed of 7 mph. Finn has to go to his locker first and leaves 15 minutes later. Finn travels at an average speed of 9mph. They arrive home at the same time. If they live 14 miles apart, how far does each one live from NJH

Answer 1

Distance between NJH and Jack's home = 7.10 miles

Distance between NJH and Finn's home = (14-7.10) = 6.9 miles

Explanation:

Given:

Jack lives east of NJH and Finn lives west of NJH.

Distance between Jack and Finn's home = 14 miles

Average speed of Jack = 7 mph

Average speed of Finn = 9 mph

Let the distance between Jack's house and NJH is '(x)' miles.

So the distance between Finn's house and NJH is '(14-x)' miles.

According to the question:

Time taken by both Finn and Jack are equal to reach home.

Considering
`t_1` is the time taken by Jack and
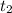`t_2` is the time taken by Finn to reach home.

So,

⇒
`t_1=t_2`

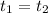
We have to find the time taken.

⇒ Time taken by Jack. ⇒ Time taken by Finn.

⇒
`t_1=(distance)/(speed)` ⇒
`t_2=(distance)/(speed)`

⇒
`t_1=(x)/(7)` mph ⇒
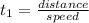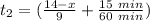`t_2=((14-x)/(9) + (15\ min)/(60\ min))` mph ...15 min extra

Equating both
`t_1` and
`t_2` :

⇒
`t_1=t_2`

⇒
`(x)/(7) =(14-x)/(9) +(1)/(4)`

⇒
`(x)/(7) =(56-4x+9)/(36)`

⇒
`(x)/(7) =(65-4x)/(36)`

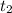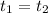
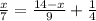
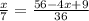
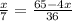
⇒ Cross multiplying.

⇒
`x(36)=7(65-4x)`

⇒
`36x=455-28x`

⇒
`36x+28x=455`

⇒
`64x=455`

⇒
`x=(455)/(64)`

⇒
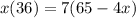
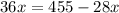
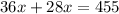
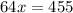
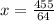
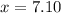`x=7.10` miles

Distance between NJH and Jack's home = (x) = 7.10 miles

Distance between NJH and Finn's home = (14-x) = (14-7.10) = 6.9 miles