Answer:
Explanation:
Given the slope-intercept form:
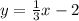
Slope-intercept form:

We substitute our x-values (-9, -3, 0, 6, and 9) for x in
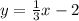 to find the y-values.
to find the y-values.
For -9:
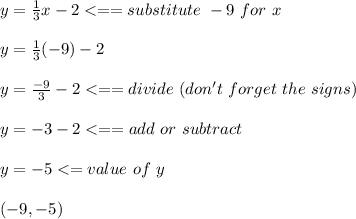
For -3:
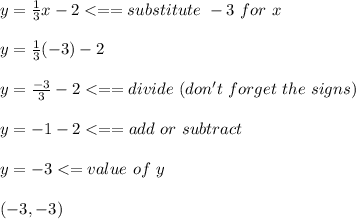
For 0:

For 6:
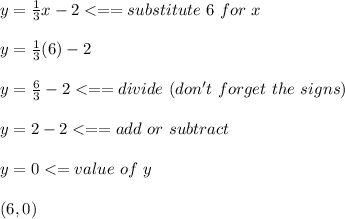
For 9:
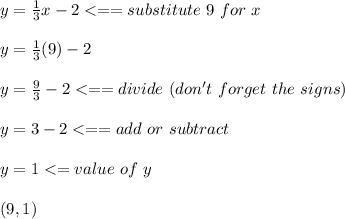
*View the attached graph to verify these answers*
Hope this helps!