Given the similarity of triangles DGH and DEF, the corresponding sides ratio
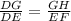 is established. Solving, x = 25, confirming the value for the given problem.
is established. Solving, x = 25, confirming the value for the given problem.
We have been given that DGH ~ DEF
According to the similarity of triangles, the ratio of corresponding sides is proportional:
![\[(DG)/(DE) = (GH)/(EF)\]](https://img.qammunity.org/2021/formulas/mathematics/college/nqr4pb0q19ubxkmmg6fcyh8gogmmtnukh9.png)
Substitute the given values:
![\[(52)/(91) = (x + 3)/(2x - 1)\]](https://img.qammunity.org/2021/formulas/mathematics/college/qeokzm6ho2okv16xjurbdvrg4xqcf4pgps.png)
Cross-multiply:
![\[(2x - 1) \cdot 52 = (x + 3) \cdot 91\]](https://img.qammunity.org/2021/formulas/mathematics/college/27x251qs7kb87wp9b5lg67sj28wdaz1258.png)
Expand:
104x - 52 = 91x + 273
Combine like terms:
104x - 91x = 273 + 52
Simplify:
13x = 325
Divide by 13:
x = 25
Therefore, the value of x is 25.