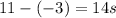Question

Its height(in meters),x seconds after takeoff, is modeled by h(x)= -(x-11)(x+3) how many seconds after takeoff will the hovercraft land on the ground

Answer 1

14s

Explanation:

1. Since the point in this question is considering the moment the hovercraft has took off, h=0 till it lands on the ground. We can do this algebraic calculation. To find the roots of the quadratic equation.

Looking at the equation:

Also, these points mark the initial and ending point of the hovercraft path. As 11 and -3 are the roots, the time between those points is the elapsed time by the hovercraft. Considering also, the x-axis, the time.

`h(x)=(-x+11)(x+3)\\h(x)=-x^(2)-3x+11x+33\\0=-x^(2)+8x+33\\\\x'=t_1=11, and\: x''=t_2=-3\\`

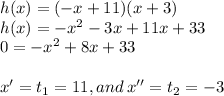
2. Graphically, we can see that movement of the hovercraft, since a< 0. The concavity is downward.

As 11 and -3 are the roots, the time between the those points, is the elapsed time by the hovercraft

`11-(-3)=14s`

Answer 2

`x = 11\,s`

Explanation:

The instants when hovercraft lands on the ground are those when h(x) = 0. Given that height function is a second-order polynomial in its factorized form, such instants are related to the roots of the function.

Time is a positive real number and the only possible solution:

`x = 11\,s`