Answer:
a) d = 2.48 cm
b)
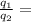 1.48 cm
1.48 cm
Step-by-step explanation:
The potential at the point
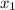 = 1.0 cm to the left of the charge is given as:
= 1.0 cm to the left of the charge is given as:
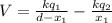
since V = 0 ; Then:
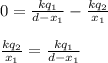
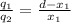
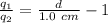
The potential at the point
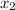 = 5.2 cm to the right of the negative charge is:
= 5.2 cm to the right of the negative charge is:
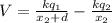
since V = 0
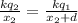
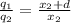
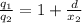
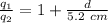
Now, let's solve for d (the distance between the charges ) from the above derived formulas
If we represent the ratio of
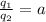
Then;
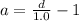
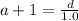
1.0a + 1 = d ------- equation (1)
Also;
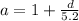
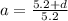
5.2 a = 5.2 +d
5.2 a - 5.2 = d ---------- equation (2)
From equation (1) ; lets replace d = 5.2 a - 5.2
then :
1.0 a + 1 = d
1.0 a + 1 = 5.2 a - 5.2
1.0a - 5.2 a = - 5.2 - 1
- 4.2 a = -6.2
a = 1.48 cm
Also replace a = 1.48 cm into equation (1) to solve for d
1.0 a + 1 = d
1.0 (1.48 )+ 1 = d
1.48 + 1 = d
d = 2.48 cm
b)
The ratio of the magnitude of the charges :
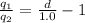
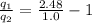
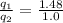
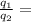 1.48 cm
1.48 cm