Answer:
Width 8 inches
Length 13 inches.
Explanation:
We have been given that a rectangle has a length that is 5 inches greater than its width and its area is 104 square inches. The equation
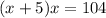 represents the situation, where x represents the width of the rectangle.
represents the situation, where x represents the width of the rectangle.
Let us solve for x to find the width of the rectangle.
Using distributive property, we will get:
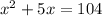
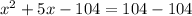
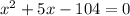
Now we will split the middle term as:

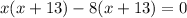
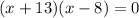
Using zero product property, we will get:
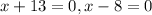
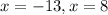
Since width cannot be negative, therefore, the width of the rectangle is 8 inches.
Length of the rectangle would be

Therefore, the length of the rectangle is 13 inches.