Answer:
a) potential energy in the spring = 1.8225 J
b) Jerry's speed = 2.744 m/s
Step-by-step explanation:
a) The spring constant, k = 1800 N/m
The rest length of the spring,
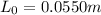
The launch length,
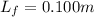
The potential energy of each spring is ,
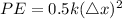
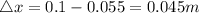
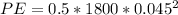
PE = 1.8225 J
b) To get Jerry's speed, use the law of energy conservation
PE energy in the string = KE of the robot
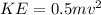
PE in the spring = 1.8225 J
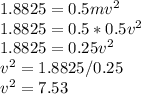
v = 2.744 m/s