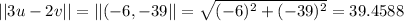Answer:

Explanation:
Vector u can also be written with initial point at the origin as:
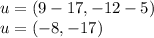
and vector v in a similar way can be written as:
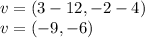
then the new vector created via the operations: 3u -2v, can be expressed as:
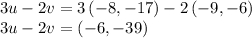
Now the norm of this vector can be found using the Pythagorean identity: