Answer:
The first four terms of the series are

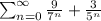 = 14.25
= 14.25
Explanation:
We know that
Sum of convergent series is also a convergent series.
We know that,
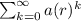
If the common ratio of a sequence |r| <1 then it is a convergent series.
The sum of the series is
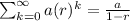
Given series,
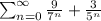
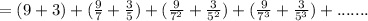
The first four terms of the series are

Let
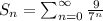 and
and
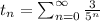
Now for
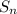 ,
,
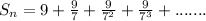
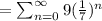
It is a geometric series.
The common ratio of
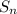 is
is

The sum of the series
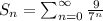
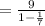
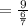
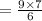
=10.5
Now for
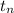
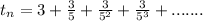
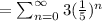
It is a geometric series.
The common ratio of
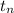 is
is
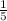
The sum of the series
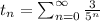

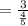
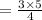
=3.75
The sum of the series is
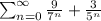
=
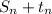
=10.5+3.75
=14.25