Question

Wo identical 7.10-gg metal spheres (small enough to be treated as particles) are hung from separate 700-mmmm strings attached to the same nail in a ceiling. Surplus electrons are added to each sphere, and then the spheres are brought in contact with each other and released. Their equilibrium position is such that each string makes a 17.0 ∘∘ angle with the vertical.

How many surplus electrons are on each sphere?

Answer 1

The number of electrons are 3.94x10¹²

Step-by-step explanation:

The translational equilibrium is:

`Tsin\theta -F_(21) =0\\Tsin\theta =F_(21)`

Dividing the expression by Tcosθ = mg

`(Tsin\theta)/(Tcos\theta ) =(F_(21) )/(mg) \\tan\theta =(F_(21) )/(mg)\\F_(21) =mg tan\theta`

The equation for electric force is:

`F_(21) =(kqq)/(d^(2) ) \\mgtan\theta =(kqq)/(d^(2) )\\q=d\sqrt{(mgtan\theta )/(k) }`

if:

`d=2Lsin\theta`

`n=(q)/(\epsilon )`

Replacing:

`n=(2Lsin\theta )/(\epsilon ) \sqrt{(mgtan\theta )/(k) }`

Where

L = 700 mm = 0.7 m

ε = 1.6x10⁻¹⁹C

m = 7.1 g = 0.0071 kg

k = 8.99x10⁹N m²/C²

Replacing:

`n=(2*0.7*sin17)/(1.6x10^(-19) ) \sqrt{(0.0071*9.8*tan17)/(8.99x10^(9) ) } =3.94x10^(12)`

Answer 2

`n = 3.94 *10^(12)`

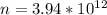
Step-by-step explanation:

Using the expression of electric force:

`F = (kq_1q_2)/(r^2)`

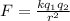
and replacing mgtanθ for F , q for
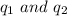`q_1 \ and \ q_2` and d for r in the relation above:

Then;

`mg tan \theta = (kqq)/(d^2)`

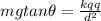
making a the subject of the formula ; we have:

`q^2 = (d^2 mg tan \theta)/(k)`

`q= \sqrt{ (d^2 mg tan \theta)/(k)}` -------------- equation (1)

By trigonometric rule:

`sin \theta = (opposite)/(hypotenuse)`

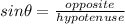
let
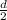`(d)/(2)` be the opposite side; and

l be the adjacent side in the above equation and solve for d:

Then

`sin \theta = (d)/(2l)`

`d = 2 \ l sin \theta`

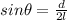
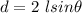
Replacing
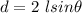`d = 2 \ l sin \theta` into equation 1 ; we have:

`q = 2\ l sin \theta \sqrt{(mgtan \theta)/(k)}`

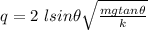
Equation for number of charge particle n =
`(q)/(e)`

So;

`n = (2 \ l sin\theta)/(e) \sqrt{(mgtan \theta)/(k)}`

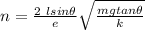
Given that :

m = 7.10 g

θ = 17.0 °

g = 9.80 m/s²

k = 8.99× 10 ⁹ N.m ²/C²

l = 700 mm

e = 1.6× 10⁻¹⁰

Then;

`n = \frac{2(700mm((10^(-3)m)/(1mm)) sin17^0 } {1.6*10^(-19)C} \sqrt{((7.10 g ((10^(-3)kg)/(1 g) (9.8 m/s^2)tan 17^0 )/(8.99*19^9 N.m^2/C^2) }`

`n = 3.94 *10^(12)`

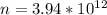
Therefore ; the number of surplus electron that are on each sphere =
`3.94 *10^(12)`