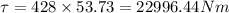Answer:
(a)

(b) I =428
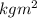
(c)
Step-by-step explanation:
GIVEN
mass = 18.2 kg
radial arm length = 3.81 m
velocity = 49.8 m/s
mass of arm = 22.6 kg
we know using relation between linear velocity and angular velocity
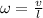
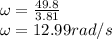
for angular acceleration, use the following equation.
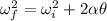
since
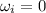
here for one circle is 2 π radians. therefore for one quarter of a circle is π/2 radians
so for one quarter
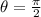
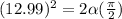
on solving

(b)
For the catapult,
moment of inertia
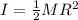
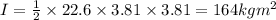
For the ball,
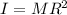
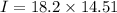
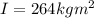
so total moment of inertia = 428
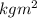
(c)