Time taken by car A = 6 hr and time taken by car B is 8 hours
Step-by-step explanation:
Given:
Distance, d = 480 km
Let x be the time taken by B to reach the destination:
So,
Time taken by car A to reach the destination = x -2
We know:
Distance = speed X time
speed =
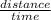
On substituting the value we get:
Speed of car A =
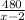
Speed of car B =
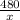
Since car A travelled 20 km/hr faster than the car B, the equation becomes:
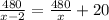
Multiplying both sides by (x - 2) we get:

Therefore, time taken by car A = x - 2
= 8 - 2 hr
= 6 hr
Time taken by car B = 8 hr