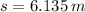Answer:
a)
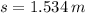 , b)
, b)
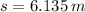
Step-by-step explanation:
a) The energy equation for the crate is modelled after the Principle of Energy Conservation and Work-Energy Theorem. Changes in gravitational potential energy can be neglected due to the information of a horizontal surface:
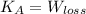

The distance that crate needs to cover before stopping is:
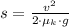
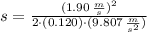
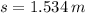
b) The stopping distance is: