Answer:
With a .95 probability, the margin of error is = 0.392
Explanation:
Given -
In order to estimate the average time spent per student on the computer terminals at a local university, data were collected for a sample of 81 business students over a one-week period.
Sample size ( n ) =81
Standard deviation
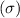 = 1.8 hours
= 1.8 hours
 = 1 -.95 =.05
= 1 -.95 =.05
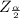 =
=
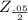 = 1.96 (Using Z table)
= 1.96 (Using Z table)
With a .95 probability, the margin of error is
Margin of error =
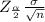
=
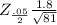
=
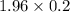
Margin of error = 0.392