Question

Help me please I’m new here

Answer 1

Given:

Composite figure made of cylinder and two spheres.

To find:

The volume of the composite solid

Solution:

Radius = 2 in

The value of π = 3.14

Volume of sphere:

`$V=(4)/(3) \pi r^3`

`$V=(4)/(3) * 3.14 * 2^3`

`$V=(4)/(3) * 3.14 * 8`

`V=33.49`

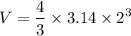
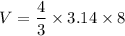
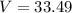
Volume of a sphere is 33.49 in³

Volume of two spheres = 2 × 33.49 = 66.98 in³

Radius of cylinder = 2 in

Height of cylinder = 8 - 2 - 2 = 4 in

Volume of cylinder:

`$V=\pi r^2 h`

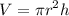
V = 3.14 × 2² × 4

V = 50.24

Volume of cylinder = 50.24 in³

Volume of composite solid = Volume of two spheres + Volume of cylinder

= 66.98 in³ + 50.24 in³

= 117.2 in³

The volume of the composite solid is 117.2 in³.