Question

A hollow spherical shell has mass 8.05kg and radius 0.215m . It is initially at rest and then rotates about a stationary axis that lies along a diameter with a constant acceleration of 0.895rad/s2 .

What is the kinetic energy of the shell after it has turned through 5.25rev ?

Express your answer with the appropriate units.

Answer 1

930.21J

Step-by-step explanation:

The kinetic energy of a solid body that is rotating, is given by:

`E_k=(1)/(2)I\omega^2`

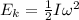
where I is the moment of inertia and w is the angular velocity.

The moment of inertia for a spherical shell is:

`I=(2)/(3)MR^2`

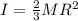
where M is the mass and R is the radius of the sphere. By replacing we have

`I=(2)/(3)(8.05kg)(0.215m)^2=0.55\ kgm^2`

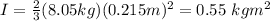
To calculate w we have to use the equation

`\omega^2=\omega_0^2+2\alpha \theta\\\\\omega=\sqrt{2(0.895rad/s^2)(5.25rev*(360\°)/(1\ rev))}=58.16(rad)/(s)`

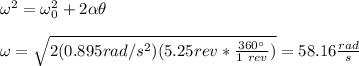
where we have taken w0=0 rad/s.

Finally, by replacing I and w we obtain:

`E_k=(1)/(2)I\omega^2 =(1)/(2)(0.55\ kgm^2)(58.16(rad)/(s))^2=930.21J`

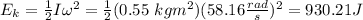
HOPE THIS HELPS!

Answer 2

Answer: The kinetic energy of the shell after it has turned through 5.25rev is 7.32J

Explanation: Please see the attachments below