Answer:
(A). 0.6828
(B). 0.9346
(C). sin (s + t) lies in the first quadrant
Explanation:
hello,
i will use
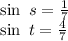
where S and t are in the third and fourth quadrant respectively.
next we find the value of cos s and cos t.
please recall that
cos x = ±
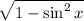
thus we have ;
cos s = ±
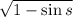
cos s = ±
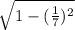
cos s = ±
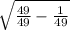
cos s = ±
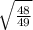
since s is in the second quadrant, we choose the negative.
cos s = -
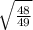
next we find cos t using the same method
cos t = ±
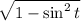
cos t =±
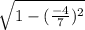
cos t = ±
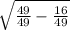
cos t = ±

since t is in the fourth quadrant, we choose the positive.
cos t =

please recall the trigonometric identity
(A) sin(A+B) = sin A cos B + sin B cos A
sin(S + t) = sin S cos t + sin t cos S
sin(S + t) =
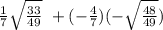
sin(S + t) =
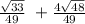
sin(S + t) =
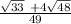
= 0.6828
(B) please recall the trigonometric identity
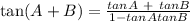 (1)
(1)
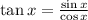
thus
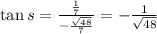
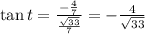
applying (1) above we have
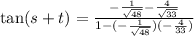
= 0.9346
(c) sin (s + t) lies in the first quadrant because its value is a positive number and sine is positive in the first or second quadrant.