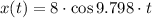Answer:
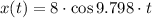
Explanation:
The equation of motion for the spring-mass system is:
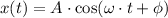
Where:

 - Spring constant, in
- Spring constant, in
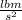 .
.
 - Mass, in
- Mass, in
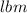 .
.
The spring constant is:
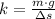
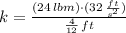
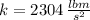
The angular frequency is:

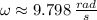
The initial condition for the system is:


The function for speed is obtained by deriving the previous function:
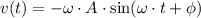
The following expressions are formed by substituting all known variables:
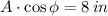
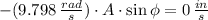
The phase angle is found by dividing the initial velocity by the initial position:
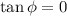
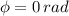
The amplitude is:
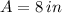
The equation of motion is: