Question

Two suppliers manufacture a plastic gear used in a laser printer. The impact strength of these gears, measured in foot-pounds, is an important characteristic. A random sample of 10 gears from supplier 1 results in x1=290 and s1=12, and another random sample of 16 gears from the second supplier results in ¯x2=321 and s2=22. Assume that both populations are normally distributed and the variances are equal. Use α=0.05.

(a) Is there evidence to support the claim that supplier 2 provides gears with higher mean impact strength?

(b) Calculate the P-value for the above test in part (a) and make a conclusion on the test.

(c) construct a 95% confidence interval estimate for the difference in mean impact strength between supplier 2 and supplier 1.

(d) Explain how the interval constructed in part (c) could be used to test the claim that the mean impact strength of gears from supplier 2 is at least 25 foot-pounds higher than that of supplier 1.

Answer 1

To test if supplier 2 provides gears with higher mean impact strength, we can conduct a two-sample t-test.

Step-by-step explanation:

To determine if there is evidence to support the claim that supplier 2 provides gears with higher mean impact strength, we can conduct a two-sample t-test. The null hypothesis (H0) is that there is no difference in mean impact strength between the two suppliers, while the alternative hypothesis (Ha) is that the mean impact strength of supplier 2 is higher than that of supplier 1.

To calculate the P-value, we need to determine the t-value and the degrees of freedom. The t-value can be calculated using the formula:

t = (x1 - x2) / sqrt((s1^2/n1) + (s2^2/n2)), where x1, x2 are the sample means, s1, s2 are the sample standard deviations, and n1, n2 are the sample sizes.

Once we have the t-value, we can determine the P-value using a t-distribution table or software. If the P-value is less than the significance level (α), we reject the null hypothesis in favor of the alternative hypothesis.

Answer 2

(a) There is enough evidence to support the claim that supplier 2 provides gears with higher mean impact strength.

(b) p-value = 0.033.

(c) The 95% confidence interval estimate for the difference in mean impact strength between supplier 2 and supplier 1 is (-64.26, 2.26).

(d) The null hypothesis is rejected.

Step-by-step explanation:

Let X₁ denotes plastic gear manufactured by supplier 1 and X₂ denotes plastic gear manufactured by supplier 2.

The given information is,

`\bar x_(1)=290\\s_(1)=12\\n_(1)=10`
`\bar x_(2)=321\\s_(2)=22\\n_(2)=16`

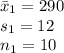
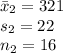
(a)

The hypothesis for the test can be defined as:

H₀: There is no difference between the mean impact strength of the gears provided by the two suppliers, i.e. μ₁ - μ₂ = 0.

Hₐ: The means impact strength of the gears provided by the supplier 2 is higher, i.e. μ₁ - μ₂ < 0.

It is assumed that the two populations are normally distributed and the variances are equal.

We will use a t-test to perform the test.

The t-statistic is given by,

`t=\frac{\bar x_(1)-\bar x_(2)}{S_(p)\sqrt{(1)/(n_(1))+(1)/(n_(2))}}`

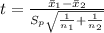
`S_(p)` = pooled standard deviation

Compute the pooled standard deviation as follows:

`S_(p)=\sqrt{((n_(1)-1)s_(1)^(2)+(n_(2)-1)s_(2)^(2))/(n_(1)+n_(2)-2)}`

`=\sqrt{((10-1)(12)^(2)+(22-1)(22)^(2))/(10+16-2)}`

`=39.98`

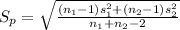
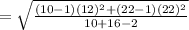
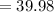
Compute the test statistic as follows:

`t=\frac{\bar x_(1)-\bar x_(2)}{S_(p)\sqrt{(1)/(n_(1))+(1)/(n_(2))}}=\frac{290-321}{39.98*\sqrt{(1)/(10)+(1)/(16)}}=-1.92`

The, t-statistic value is -1.92.

The degrees of freedom of the test is:

df = (n₁ + n₂ - 2) = 24

Decision rule:

If the test statistic value is less than the critical value then the null hypothesis will rejected.

The critical value is:

`t_{\alpha, (n_(1)+n_(2)-2)}=t_(0.05, 24)=-1.71`

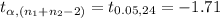
*Use a t-table.

The test statistic value is less than the critical value.

Thus, the null hypothesis will be rejected at 5% level of significance.

So, there is enough evidence to support the claim that supplier 2 provides gears with higher mean impact strength.

(b)

For the computed t-statistic and (n₁ + n₂ - 2) degrees of freedom, the p-value will be,

`p-value =P(t_(0.05,24)>-1.92)=0.033`

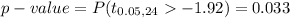
Use the t-table.

The p-value of the test is less than the significance level . Thus, the null hypothesis is rejected.

Concluding that there is enough evidence to support the claim that supplier 2 provides gears with higher mean impact strength.

(c)

The 95% confidence interval is:

`CI=(\bar x_(1)+\bar x_(2))\pm t_{\alpha, (n_(1)+n_(2)-2}* S_(p)\sqrt{(1)/(n_(1))+(1)/(n_(2))}`

`=(290-321)\pm 2.064* 39.98\sqrt{(1)/(10)+(1)/(16)}\\=-31\pm33.26\\=(-64.26, 2.26)`

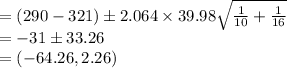
Thus, the 95% confidence interval estimate for the difference in mean impact strength between supplier 2 and supplier 1 is (-64.26, 2.26).

(d)

A confidence interval can be used to test the claim made.

If the confidence interval consist the null value of the parameter then the null hypothesis will be accepted or else rejected.

The alternate hypothesis to be tested is:

Hₐ: The mean impact strength of gears from supplier 2 is at least 25 foot-pounds higher than that of supplier 1, i.e. μ₁ - μ₂ ≥ - 25

The 95% confidence interval estimate for the difference in mean impact strength consist the difference values less than 25 foot-pounds.

Thus, the null hypothesis is rejected.