Question

A particular reactant decomposes with a half-life of 121 s when its initial concentration is 0.357 M. The same reactant decomposes with a half-life of 235 s when its initial concentration is 0.184 M.

What is the value and unit of the rate constant for this reaction?

Answer 1

Answer : The value and unit of the rate constant for this reaction is,
`2.31* 10^(2)` and
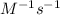`M^(-1)s^(-1)` respectively.

Explanation :

As we know that half-life of zero-order and second-order reaction depend on the concentration of reactant while the half-life of first-order reaction is independent of the concentration of the reactant.

The expression of half-life for zero order reaction:

`t_(1/2)=([A_o])/(2k)`

The expression of half-life for first order reaction:

The expression of half-life for second order reaction:

`t_(1/2)=(1)/([A_o]k)`

The given reaction can not be first order reaction because it is independent of the concentration of the reactant.

So, the given reaction can be zero order or second order.

First we have to calculate the value of rate constants for zero order.

`t_(1/2)=([A_o])/(2k)`

`121s=(0.357M)/(2k)`

`k=1.48* 10^(-3)M/s`

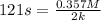
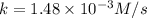
and,

`t_(1/2)=([A_o])/(2k)`

`235s=(0.184M)/(2k)`

`k=3.92* 10^(-4)M/s`

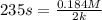
From this we conclude that the reaction can not be zero order.

Now we have to calculate the value of rate constants for second order.

`t_(1/2)=(1)/([A_o]k)`

`121s=(1)/((0.357M)* k}`

`k=2.31* 10^(2)M^(-1)s^(-1)`

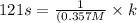
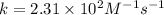
and,

`t_(1/2)=(1)/([A_o]k)`

`235=(1)/((0.184M)* k}`

`k=2.31* 10^(2)M^(-1)s^(-1)`

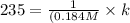
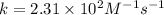
From this we conclude that the reaction is a second order.

Therefore, the value and unit of the rate constant for this reaction is,
`2.31* 10^(2)` and
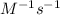`M^(-1)s^(-1)` respectively.