Answer:
v = 376.06 mph , θ = 41.23º
Step-by-step explanation:
This exercise can be solved with the addition of vectors, we have two vectors: the speed of the airplane 400 mph in the 45 direction to the north east and the speed of the wind coming from the north, therefore the wind direction is south.
One way to solve these exercises is to use trigonometry to break down the speed of the plane.
v₁ₓ = v₁ cos 45
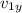 = v₁ sin45
= v₁ sin45
v₁ₓ = 400 0.707
v₁ₓ = 282.84 mph
v_{1y} = 282.84 mph
Wind speed is
v₂ = 35 mph
Let's add each speed
vₓ = v₁ₓ
vₓ = 282.84 mph
v_{y} = v_{1y} - v₂
v_{y} = 282.84 - 35
v_{y} = 247.84 mph
The result can be done in two ways
v = (282.84 i ^ + 247.84 j ^) mph
And in the form of a module and angle, for which we use the Pythagorean theorem and trigonometry
v = √ (vₓ²+ v_{y}²)
v = √ (282.84² + 247.84²)
v = 376.06 mph
tan θ = v_{y} / vₓ
θ = tan⁻¹ (247.84 / 282.84)
θ = 41.23º