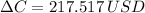Answer:
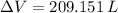 ,
,
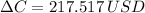
Step-by-step explanation:
The drag force is equal to:
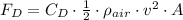
Where
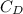 is the drag coefficient and
is the drag coefficient and
 is the frontal area, respectively. The work loss due to drag forces is:
is the frontal area, respectively. The work loss due to drag forces is:
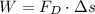
The reduction on amount of fuel is associated with the reduction in work loss:
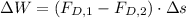
Where
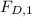 and
and
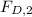 are the original and the reduced frontal areas, respectively.
are the original and the reduced frontal areas, respectively.
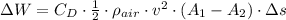
The change is work loss in a year is:
![\Delta W = (0.3)\cdot \left((1)/(2)\right)\cdot (1.20\,(kg)/(m^(3)))\cdot (27.778\,(m)/(s))^(2)\cdot [(1.85\,m)\cdot (1.75\,m) - (1.50\,m)\cdot (1.75\,m)]\cdot (25* 10^(6)\,m)](https://img.qammunity.org/2021/formulas/engineering/college/8emip8jnvfdhjynhtrq9ii4keeevmxzqh6.png)
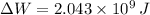
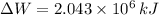
The change in chemical energy from gasoline is:
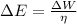
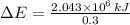
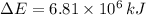
The changes in gasoline consumption is:
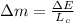
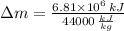
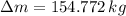
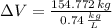
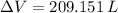
Lastly, the money saved is: