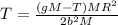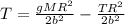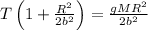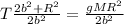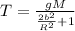Answer:
Step-by-step explanation:
If we ignore the thickness of the string, then the tension T of the string on the yoyo would cause a torque with a magnitude of Tb. This torque would then generate an angular acceleration according to Newton's 2nd law:
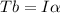
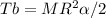
We can substitute angular acceleration as ratio of linear acceleration and spool radius
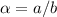
Therefore

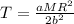
The system has 2 forces, gravity pulling it down and tension force upward. The net force would generate the linear acceleration a

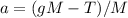
now we can substitute for a into the tension equation