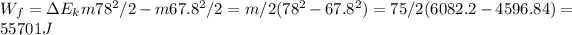Question

A rope is tied to a tree limb and is used by a swimmer to swing into the water. The person starts from rest with the rope held in the horizontal position, swings downward and then let go of the rope. His initial height is h0 = 415 m and final height is hf = 105 m. If the force due to air resistance is neglected,

What is the total work done on the person by the tensional force of the rope?



What is the speed of the swimmer as he let go of the rope?



If the speed of the swimmer is measured to be 67.8 m/s, and the mass of the swimmer is 75.0 kg, find the total work done on the swimmer by the frictional force – air resistance during this swinging process.

Answer 1

Tension force does no work

78 m/s

55701 J

Step-by-step explanation:

The work done by the tension force of the rope is the dot product of the tension force vector and the distance travel vector as he swings. However, as these 2 vectors are always perpendicular to each other, their dot product would be 0 (cos(90) = 0). So the work done by tension force is 0.

If we neglect air resistance, then only gravity does work on the swimmer. We can apply the following energy conservation equation to calculate the kinetic energy once we let go of the rope.

`E_p = E_k`

`mg\Delta h = mv^2/2`

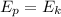
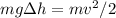
where m is the mass of the swimmer, g = 9.81 m/s2 is the gravitational constant, Δh = 415 - 105 = 310 m is the height difference as he swings from horizontal point to the let go point. v is the let go speed. We can divide both sides by m

`g \Delta h = v^2/2`

`v^2 = 2g \Delta h = 2*9.81*310 = 6082.2`

`v = √(6082.2) = 78 m/s`

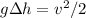
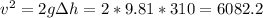
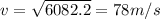
If the swimmer actually end up with only 67.8 m/s, then the loss in kinetic energy is due to air resistance during the swinging process. We can also find this by calculating the difference between the kinetics energies

`W_f = \Delta E_k m78^2/2 - m67.8^2/2 = m/2(78^2 - 67.8^2) = 75/2(6082.2 - 4596.84) = 55701 J`