Answer: The pressure inside the bottle is 2473 kPa
Step-by-step explanation:
Combined gas law is the combination of Boyle's law, Charles's law, Avogadros law and Gay-Lussac's law.
The combined gas equation is,
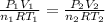
where,
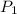 = initial pressure of gas = 4120 kPa
= initial pressure of gas = 4120 kPa
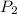 = final pressure of gas = ?
= final pressure of gas = ?
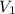 = initial volume of gas = v
= initial volume of gas = v
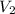 = final volume of gas = v
= final volume of gas = v
 = initial moles of gas = n
= initial moles of gas = n
 = final moles of gas =
= final moles of gas =
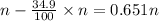
 = initial temperature of gas =
= initial temperature of gas =
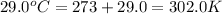
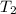 = final temperature of gas =
= final temperature of gas =

Now put all the given values in the above equation, we get:
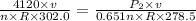
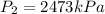
Thus the pressure inside the bottle, if 34.9 percent of the gas is released and the temperature of the gas drops to 5.5 °C is 2473 kPa