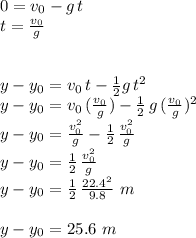Question

A kickball is kicked straight up at a speed of 22.4m/s. how high does it go

Answer 1

the kickball goes straight up 25.6 meters

Step-by-step explanation:

We are in the case of motion under constant (uniform) acceleration. This is an object with initial velocity pointing strictly upwards, under th acceleration of gravity which slows down its motion. The projectile keeps losing velocity as it moves upward until its velocity is zero when it stops moving upwards, and starts falling also under accelerated motion and gaining downward velocity as time goes by.

We use he formula for displacement under accelerated motion (due to gravity "g" opposing the initial velocity):

`y-y_0=v_0\,t-(1)/(2) g\,t^2`

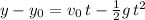
and also the formula for the velocity in terms of time:

`v(t)=v_0-g\,t`

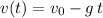
Using that the initial velocity is 22.4 m/s, g = 9.8 m/s^2 , and the fact that we want the time "t" at which the velocity v(t) = 0 (zero), we solve for "t" in the second equation, and use it to substitute for "t" in the first one:

`0=v_0-g\,t\\t=(v_0)/(g) \\\\\\y-y_0=v_0\,t-(1)/(2) g\,t^2\\y-y_0=v_0\,((v_0)/(g))-(1)/(2) \,g\,((v_0)/(g))^2\\y-y_0=(v_0^2)/(g) -(1)/(2)\,(v_0^2)/(g)\\y-y_0=(1)/(2)\,(v_0^2)/(g)\\y-y_0=(1)/(2)\,(22.4^2)/(9.8)\,\,m\\\\y-y_0=25.6\,\,m`