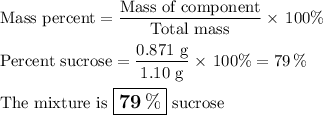Question

A 1.10 g sample contains only glucose and sucrose. When the sample is dissolved in water to a total solution volume of 25.0L, the osmotic pressure of the solution is 3.78 atm at 298k. What is mass percent sucrose?

Answer 1

`\large \boxed{79 \, \%}`

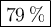
Step-by-step explanation:

I assume the volume is 2.50 L. A volume of 25.0 L gives an impossible answer.

We have two conditions:

(1) Mass of glucose + mass of sucrose = 1.10 g

(2) Osmotic pressure of glucose + osmotic pressure of sucrose = 3.78 atm

Let g = mass of glucose

and s = mass of sucrose. Then

g/180.16 = moles of glucose, and

s/342.30 = moles of sucrose. Also,

g/(180.16×2.50) = g/450.4 = molar concentration of glucose. and

s/(342.30×2.50) = s/855.8 = molar concentration of sucrose.

1. Set up the osmotic pressure condition

Π = cRT, so

`\begin{array}{rcl}\Pi_{\text{g}} +\Pi_{\text{s}}&=&\Pi_{\text{tot}}\\(g)/(450.4)*8.314*298 + (s)/(855.8)*8.314*298 & = & 3.78\\\\5.501g + 2.895s & = & 3.78\\\end{array}`

Now we can write the two simultaneous equations and solve for the masses.

2. Calculate the masses

`\begin{array}{lrcl}(1)& g + m & = & 1.10\\(2) &5.501g +2.895s & = & 3.78\\(3) & m & = &1.10 - g\\&5.501g + 2.895(1.10 - g) & = & 3.78\\&2.606g + 3.185 & = & 3.78\\ &2.606g & = & 0.595\\(4) & g & = & \mathbf{0.229}\\&0.229 + s & = & 1.10\\& s & = & \mathbf{0.871}\\\end{array}`

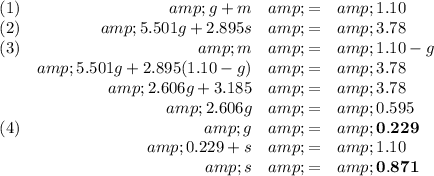
We have 0.229 g of glucose and 0.871 g of sucrose.

3. Calculate the mass percent of sucrose

`\text{Mass percent} = \frac{\text{Mass of component}}{\text{Total mass}} * \, 100\%\\\\\text{Percent sucrose} = \frac{\text{0.871 g}}{\text{1.10 g}} * \, 100\% = 79 \, \%\\\\\text{The mixture is $\large \boxed{\mathbf{79 \, \%}}$ sucrose}`