Question

Need to find the area of the figure

Answer 1

Given:

`a=4√(3)`

To find:

The area of the figure

Solution:

The given figure is regular hexagon.

Number of sides = 6

Using apothem formula:

`$a=(s)/(2 \tan \left((180^\circ)/(n)\right))`

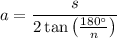
where a is apothem, s is side length and n is number of sides of the polygon.

`$4√(3) =(s)/(2 \tan \left((180^\circ)/(6)\right))`

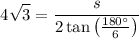
Multiply by 2 on both sides.

`$8√(3) =\frac{s}{ \tan {30^\circ}}`

`$8√(3) =(s)/( (1)/(√(3) ) )`

`$8√(3) =\frac{s{√(3) }}{ 1 }`

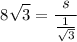
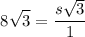
Cancel the common factor
`√(3)` on both sides, we get

`8=s`

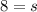
Side length of the polygon = 8 units

Area of the polygon:

`$A=(1)/(2) * ( \text {apothem }* \text{ perimeter})`

`$A=(1)/(2) * ( 4√(3) * 6* 8)`

`$A=96√(3)`

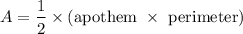
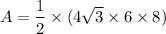
A = 166.27 in²

The area of the figure is 166.27 in².