Answer:
Part A =
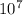
Part B =
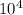
Part C = 5040
Part D = 50.4%
Explanation:
Part A
You need to choose 7 digits of a number and you can choose freely from 0-9 (10 possible ways). There are no rules that you have to follow for this part. We can assume that all digits of the number is independent and the order is important.
Since the number is independent, all digit will have 10 possible numbers. The order is important so you don't need to use a combination. The calculation of the possible ways to make the phone number will be:
number of possible ways = possible choice^digit of number= 10^7=
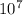
Part B
In part B, you have to fulfill a condition/rule that the start of the number has to be 772. The number will have 772 prefixes so it should look like this
772 _ _ _ _
We still have 4 empty slots out of 7 digits. There are no other rules for this number, so we can use the same formula as part A.
number of possible ways= possible choice^digit of number= 10^4=
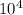
Part C
This part adds more conditions/rules. Now the last 4 free digits can't have repeating numbers. This means that the choice for the first digit will limit/influence other digits. The first digit will have 10 possible ways, but the second digit will have 9 possible ways since they can't be duplicated. So, the digit will be dependent.
Since the event is dependent, we need to use permutation instead of simply put the number of the digit as an exponent. The calculation will become:
number of possible ways=(possible choice)!/(possible choice-digit of number)!
number of possible ways=10!/(10-4)!= 10!/6! = 5040
Part D
In this part, we are calculating a conditional probability.
We want to know the chance that the number has none of its 4 digit repeating(X), let's say its P(X).
The condition is that the number has prefix 772(Y). This condition will be similar to the question in part B, we will call the possible ways as P(Y).
P(Y)=
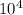
Notice that the question at part C has the condition of X(four digits not repeating), and Y(prefix 772) we will call the possible ways as P(X ∩Y).
P(X ∩Y)= 5040
The formula for conditional probability is
P(X|Y)= P(X ∩Y)/P(Y) = 5040/ 10,000= 0.504= 50.4%