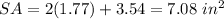Answer:
Explanation:
we know that
The Cavalieri's principle states that if two solids are of equal height and the sections "matching" equal areas everywhere along the height, the solids have the same volume.
The surface area of the stack is given by the formula
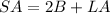
where
B is the area of the base
LA is the lateral area
The lateral area of the stack, using Cavalieri's Principle, is equal to the lateral area of one CD multiplied by the total number of CDs of the stack
so
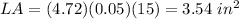
Find the radius of CD
Remember that the circumference is given by the formula

we have

substitute
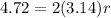
solve for r
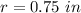
Find the area of CD
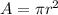
substitute
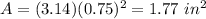
therefore
The surface area of the stack is equal to