Question

The volume of a cylinder is 30 pie cubic units. A cone shares the same base. The height of the cone is twice the height of the cylinder. What is the volume of the cone?

Choices: A.5 pie B. 15 pie C. 20 pie D. 45 pie E. 60 pie

Answer 1

Given:

The volume of a cylinder is
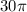`30 \pi` cubic units.

A cone shares the same base.

The height of the cone is twice the height of the cylinder.

We need to determine the volume of the cone.

Height of the Cone:

Let h denote the height of the cylinder.

Let H denote the height of the cone.

Since, it is given that, the height of the cone is twice the height of the cylinder, we have;

`H=2h`

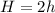
Volume of the cylinder:

The formula to determine the volume of the cylinder is

`V=\pi r^2 h`

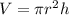
Since, volume of the cylinder is
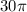`30 \pi`, we get;

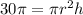`30 \pi = \pi r^2 h` -------(1)

Volume of the cone:

The formula to determine the volume of the cone is

`V=(1)/(3) \pi r^2 H`

Substituting
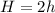`H=2h`, we get;

`V=(1)/(3) \pi r^2 (2h)`

`V=(2)/(3) \pi r^2 h`

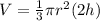
Substituting equation (1), we get;

`V=(2)/(3) (30 \pi)`

`V=20 \pi`

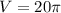
Thus, the volume of the cone is 20π

Hence, Option C is the correct answer.