Question

In the figure to the right, if AC=19 and BC=16, what is the radius?

*For a circle*

Answer 1

The radius of the circle is 10.2 units

Explanation:

The complete question is

In the figure to the right, if AC=19 and BC=16, what is the radius?

A circle has center A. Points B and D are on the circle, with B on the left and D near the bottom. Point C lies outside the circle such that the line segment A C passes through point D and the line segments A B and B C form a right angle.

The radius is approximately (Round to the nearest tenth as needed.)

The picture of the question in the attached figure

we know that

In the right triangle ABC

Applying the Pythagorean Theorem

`AC^2=AB^2+BC^2`

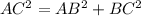
substitute the given values

`19^2=AB^2+16^2`

solve for AB

`AB^2=19^2-16^2`

`AB^2=105\\AB=10.2\ units`

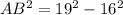
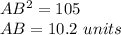
Remember that the radius is the same that the segment AB

therefore

The radius of the circle is 10.2 units