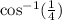Question

Find all solutions in the interval [0, 2π).
2 sin2x = sin x

Answer 1

The solutions on the given interval are :

`0`

`\pi`

`\cos^(-1)((1)/(4))`

`-\cos^(-1)((1)/(4))+2\pi`

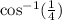
Explanation:

We will need the double angle identity
`\sin(2x)=2\sin(x)\cos(x)`.

Let's begin:

`2\sin(2x)=\sin(x)`

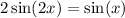
Use double angle identity mentioned on left hand side:

`2\cdot 2\sin(x)\cos(x)=\sin(x)`

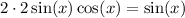
Simplify a little bit on left side:

`4\sin(x)\cos(x)=\sin(x)`

Subtract
`\sin(x)` on both sides:

`4\sin(x)\cos(x)-\sin(x)=0`

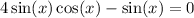
Factor left hand side:

`\sin(x)[4\cos(x)-1]=0`

Set both factors equal to 0 because at least of them has to be 0 in order for the equation to be true:

`\sin(x)=0 \text{ or } 4\cos(x)-1=0`

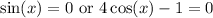
The first is easy what angles
`\theta` are
`y`-coordinates on the unit circle 0. That happens at
`0` and
`\pi` on the given range of
`x` (this
`x` is not be confused with the
`x`-coordinate).

Now let's look at the second equation:

`4\cos(x)-1=0`

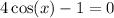
Isolate
`\cos(x)`.

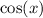Add 1 on both sides:

`4 \cos(x)=1`

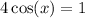
Divide both sides by 4:

`\cos(x)=(1)/(4)`

This is not as easy as finding on the unit circle.

We know
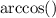`\arccos( )` will render us a value between
`0` and
`2\pi`.

So one solution on the given interval for x is
`x=\cos^(-1)((1)/(4))`.

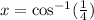We know cosine function is even.

So an equivalent equation is:

`\cos(-x)=(1)/(4)`

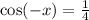
Apply
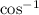`\cos^(-1)` to both sides:

`-x=\cos^(-1)((1)/(4))`

Multiply both sides by -1:

`x=-\cos^(-1)((1)/(4))`

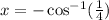
This going to be negative in the 4th quadrant but if we wrap around the unit circle,
`2\pi` , we will get an answer between
`0` and
`2\pi`.

So the solutions on the given interval are :

`0`

`\pi`

`\cos^(-1)((1)/(4))`

`-\cos^(-1)((1)/(4))+2\pi`