Question

Consider the following function.
Which table shows correct values for the function?

Answer 1

Given:

`f(x)=-4 \sqrt[3]{x}+6`

To find:

Which table shows correct values for the function.

Solution:

Substitute x = -8 in the function:

`f(-8)=-4 \sqrt[3]{-8}+6`

Apply radical rule:
`\sqrt[n]{-a}=-\sqrt[n]{a}`, if n is odd.

`f(-8)=-(-4 \sqrt[3]{8})+6`

`f(-8)=4 \sqrt[3]{2^3}+6`

`f(-8)=4 (2)+6`

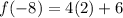
f(-8) = 14

Substitute x = -1 in the function:

`f(-8)=-4 \sqrt[3]{-1}+6`

Apply radical rule:
`\sqrt[n]{-a}=-\sqrt[n]{a}`, if n is odd.

`f(-1)=-(-4 \sqrt[3]{1})+6`

`f(-1)=4 \sqrt[3]{1^3}+6`

`f(-1)=4 (1)+6`

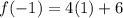
f(-8) = 10

Substitute x = 0 in the function:

`f(0)=-4 \sqrt[3]{0}+6`

`f(0)=0+6`

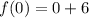
f(0) = 6

Substitute x = 8 in the function:

`f(8)=-4 \sqrt[3]{8}+6`

`f(8)=-4 \sqrt[3]{2^3}+6`

`f(8)=-4 (2)+6`

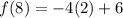
f(8) = -2

Therefore table 3 is shows correct values for the function.