Given:
In circle O, CD = 56, OM = 20, ON = 16
CD is perpendicular OM and EF is perpendicular to ON
Solution:
The reference image for the answer is attached below.
Part a: Join OC, we get triangle OCM.
OM bisects CD.
CM = MD =
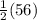 = 28
= 28
Using Pythagoras theorem:


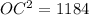
Taking square root on both sides.
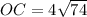
The radius of the circle is 4√74.
Part b: Join FO, we get triangle FON.
Since radius is
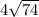 ,
,
 .
.
Using Pythagoras theorem:

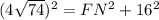
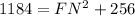
Subtract 256 from both sides.
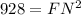
Taking square root on both sides.
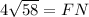
Therefore, FN = 4√58
Part c: ON bisects EF.
FN = EN = 4√58
EF = FN + EN
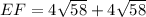
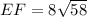
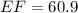
Therefore, EF = 60.9.