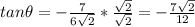Answer:
Explanation:
Sin theta is the ratio of side opposite over hypotenuse of a reference angle situated at the origin in an x-y coordinate plane. If sec theta is negative, then the only quadrant where sin is positive AND sec is negative is quadrant 2. Remember that sec theta is the inverse of cos theta. Puttling our right triangle in QII, the side measuring 7 is across from the angle and the hypotenuse is 11. In order to find the cos theta and tan theta, we need the side adjacent to the angle. Use Pythagorean's Theorem to find the side adjacent.
 and
and
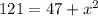 and
and
 so
so
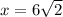
Remember that this value is why the sec is negative. Because x is negative in QII, the cos theta is side adjacent over hypotenuse:
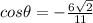 and
and

But we should probably rationalize that denominator, so