Question

Question 4

1 pts
The stopping distance d of an automobile is directly proportional to the square of its
speed s. On one road, a car requires 75 feet to stop from a speed of 30 miles per hour.
How many feet does the car require to stop from a speed of 48 miles per hour on the
same road?

Answer 1

The car requires 192 ft to stop from a speed of 48 mph

Step-by-step explanation:

Given:

Speed, u = 30 mph

Stopping distance, d = 75 feet

The stopping distance d of a car after the brakes are applied varies directly as the square of the speed, u

So,

d = k (u)²

On substituting the value:

75 = k (30)²

k =
`(75)/(900) (ft hr^2)/(miles^2)`

Speed, u₂ = 48 mph

d₂ = ?

d₂ = k (u₂)²

On substituting the values we get:

d₂ =
`(75)/(900) X (48)^2`

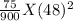
d₂ = 192 ft