Question

PLEASE HELP quickly with these two problems

1) the following system of equations, complete a table of at least 5 points for each equation, then graph the system on the coordinate plane. Describe the solution.
y = -3x + 4
6x + 2y - 8 = 0

2) Graph the following system of linear inequalities. Identify at least two points in the solution:
y < 5 - 2x
x + 5y > -7

Answer 1

Here's what I get.

Explanation:

Question 1

(1) y = -3x + 4

(2) 6x + 2y - 8 = 0

Solve equation (2) for y.

2y = 8 - 6x

(3) y = 4 - 3x

Below are five points for Equations (1) and (3}

`\begin{array}rr\mathbf{x} & \mathbf{y} & \mathbf{x} & \mathbf{y}\\-2 & 10 & -2 & 10\\-1&7 & -1 & 7\\0&4 & 0 & 4\\1 & 1 &1&1\\2 & -2 & 2&-2\\\end{array}\\`

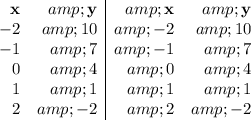
In the first diagram below, the two graphs coincide.

There is an infinite number of solutions to the system of equations.

Question 2

(4) y < 5 - 2x

(5) x + 5y > -7

Solve equation (3) for y

5y > -x - 7

(6) y > -⅕(x + 7)

Below are five points for each of Equations (4) and (5}

`\begin{array}rr\mathbf{x} & \mathbf{y} & \mathbf{x} & \mathbf{y}\\& & -7 & 0\\& & -2 & -1\\0&5 & & \\2 & 1 &&\\& & 3&2\\4&-3 & &\\6&-7 & &\\8&-11 & 8&-3\\& & 13&-4\\\end{array}\\`

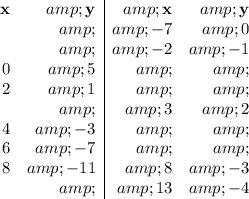
In the second diagram below, all points above the dashed red line satisfy Equation(4).

All points below the dashed blue line satisfy Equation (5).

All points in the overlapping purple area satisfy both inequalities.

Two of these points are (0,0) and (2,0).